@AutoWired

@Autowired

• 필요한 의존 객체의 ‘타입’에 해당하는 빈을 찾아 주입한다.

사용 할 수 있는 위치

• constructor (스프링 4.3부터는 생략가능)
• setter
• field

경우의 수

• 해당 타입의 빈이 없는 경우
  • 실패
• 해당 타입의 빈이 한 개인 경우
  • 성공
• 해당 타입의 빈이 여러 개인 경우
  • 빈 이름으로 시도
    • 같은 이름의 빈 찾으면 해당 빈 사용
    • 같은 이름 못 찾으면 실패

같은 타입의 빈이 여러 개 일때

• @Primary
• 해당 타입의 빈 모두 주입 받기
• @Qualifier(빈 이름으로 주입)

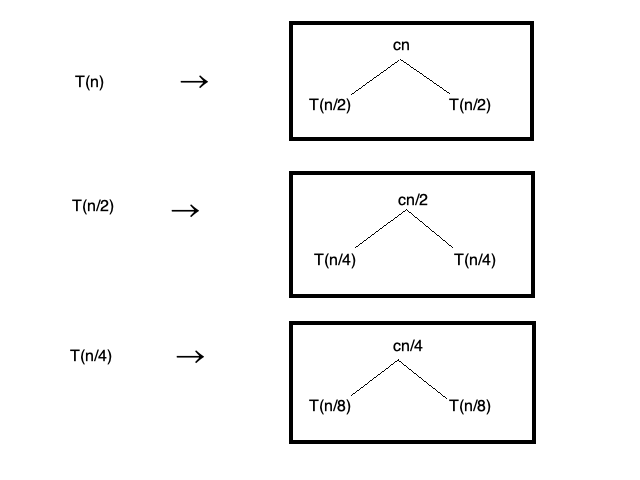
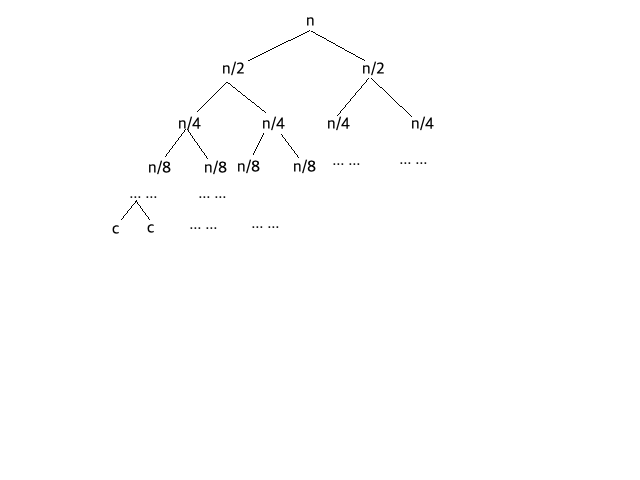
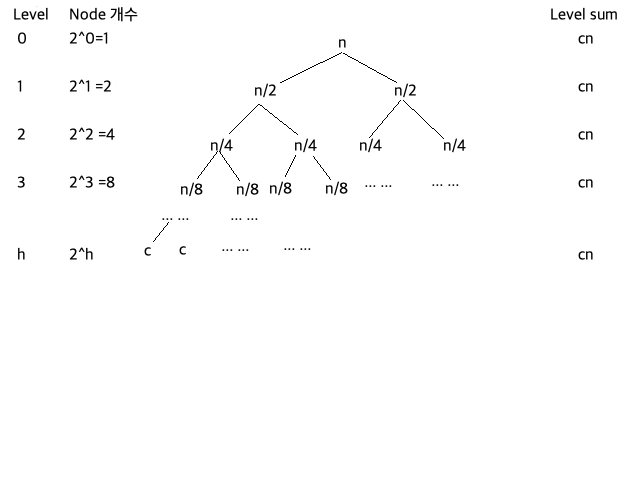
동작 원리

• BeanPostProcessor

  • 새로 만든 빈 인스턴스를 수정할 수 있는 라이프 사이클 인터페이스

• AutowiredAnnotationBeanPostProcessor extends BeanPostProcessor

  • 스프링이 제공하는 @Autowired와 @Value 애노테이션

    그리고 JSR-330의 @Inject 애노테이션을 지원하는 애노테이션 처리기

ref. spring.io

ref. 스프링 프레임워크 핵심 기술

12/10 화요일

1. Spring

   • 스프링 프레임워크 핵심 기술 IoC 컨테이너 1부~3부 강의 정리하였다.

###생성자 주입을 사용해야하는 이유

DI의 종류

• Field Injection(by @Autowired) (필드 주입)
• Setter Injection (수정자 주입)

• Constructor Injection (생성자 주입)

• 생성자 주입의 장점

  • 1. NPE 방지

       필드 주입과 수정자 주입의 경우

       의존하는 객체를 주입받지 못하여 NPE가 발생할 수 있지만

       생성자 주입은 객체 생성시 의존하는 객체르 주입 받아 이를 방지 할 수 있다.

  • 1. 순환참조 방지

  ​ A,B 객체가 서로에게 의존하는 상황이라고 가정하자.

  ​ 생성자 주입으로 A객체에서 B객체를, B객체에서 A객체를 주입 받는다면

  ​ 애플리케이션이 시작하기 전에 순환참조임을 알려주므로

  ​ 스택오버플로우를 사전에 방지할 수 있다.

  @Service
  public class A {
    
      private B b;
    
      @Autowired
      public A(B b) {
          this.b = b;
      }
        
      public void thisIsAMethod() {
          b.thisIsBMethod();
      }
  }
    
  @Service
  public class B {
    
      private A a;
    
      @Autowired
      public B(A a) {
          this.a = a;
      }
    
      @Override
      public void thisIsBMethod() {
          a.thisIsAMethod();
      }
  }
  

  • 1. 테스트 코드 작성이 용이하다.

       필드 주입의 경우 스프링 컨테이너에 의존적이므로

       스프링과 관련된 애너테이션을 사용하지 않고는 주입할 방법이 없다.

       그에 비해 생성자 주입은 생성 시 필요한 객체들을 주입해주므로 POJO답게 객체를 사용할 수있다.

12/09 월요일

1. Spring

   • DI 종류와 생성자를 사용해야 하는 이유를 포스팅 하였다

2. 알고리즘

   • Introduction to Algorithm
     • 힙 자료구조와 힙정렬에 대해 학습하였으나 시간이 부족하여 완전히 이해하지 못하였다

3. 내일 할 일

   • 힙정렬과 힙에 대한 내용 정리

합병 정렬 시간복잡도 분석

• 입력크기가 n인 배열의 정렬 수행시간을 T(n)이라 하자.

T(n)에 대한 점화식은 다음과 같다.

T(n) = cn ( n = 1 )

T(n) = 2T(n/2) + cn ( n>1 )

T(n)이 2T(n/2) + cn (n>1)인 이유

T(n/2) : n을 divide & conquer 하는 과정

cn : divide & conquer 후 merge하는 데 드는 비용

c : 연산시간, n: 입력크기

• 점화식을 트리구조로 표현하면 다음과 같다.

위 그림에서 T(n)을 표현한 트리에서 T(n/2), T(n/4)을 대입하면 다음과 같다.

트리의 각 레벨에서 노드의 개수와 각 레벨의 합을 구하면 아래와 같다.

Level 0 에는 n이 1개 있고, level 1 에는 n/2 이 2개, level 2 에는 n/4 이 4개, … , level h 에는 T(1) 이 2^h 개 있다. T(1) = 1 로 표현 가능하므로 h = log2n 이라는 결과를 얻을 수 있다.

2^h * c = cn
2^h = n
h = logn

각 레벨 합이 cn이 트리의 높이 logn 만큼 있으므로
시간 복잡도 = O(nlogn) (c는 상수이므로 생략)