New IO

23 Mar 2020 | Java

JAVA NIO (New IO)

Overview

1. 채널과 버퍼

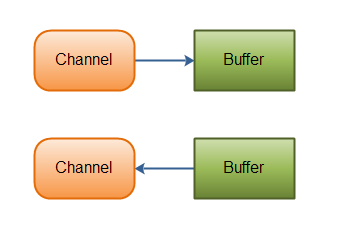
IO API는 byte stream과 character stream을 사용하지만 NIO API는 channel과 buffer 를 사용한다.

데이터는 항상 채널에서 버퍼로 읽혀지고, 버퍼에서 채널로 쓰여진다.

buffer-oriented

1. 버퍼를 이용함으로서 데이터를 캐싱할 수 있다

2. read/write 과정을 추적하고 부가적인 작업(전처리/후처리)를 하기에 용이하다.

3. 버퍼에 read/write 작업 전에 버퍼가 비었는지 확인하는 작업이 필요하다

2. Non-blocking IO

자바 NIO에서는 non-blocking IO가 가능하다. 예를들어 하나의 스레드는 채널에게 버퍼에 데이터를 읽어오도록 시킬 수 있 고 채널이 데이터를 버퍼로부터 읽는 동안 스레드는 다른 작업을 수행할 수 있다. 데이터가 채널에서 버퍼로 읽혀지면, 스레드를 해당 버퍼를 이용한 process를 계속할 수 있다. write 경우도 마찬가지다.

3. Selectors

Selector는 기본적으로 epoll 기반으로 동작하며, 커널 버전이 2.6 이하라면 poll 방식으로 동작한다

자바 NIO에는 Selector 라는 개념이 존재한다. Selector는 여러 채널에 이벤트( connection opened, data arrived )가 발생하는 것을 감시하는 모니터 객체다. 그래서 하나의 스레드에서 여러 채널에 대해 모니터링이 가능하다 ( 멀티플렉싱 )

핵심 컴포넌트

1. 채널

모든 NIO에서 IO는 채널로 시작한다. 채널은 Stream과 유사하다.

하지만 버퍼를 통해서 데이터를 읽고 쓸 수 있다는 차이점이 있다.

Java NIO: Channels and Buffers

몇 가지 핵심적인 Channel을 살펴보자면 아래와 같다.

FileChannel - 파일에 데이터를 읽고 쓴다
DatagramChannel
- UDP를 이용해 데이터를 읽고 쓴다
SocketChannel
- TCP를 이용해 데이터를 읽고 쓴다
ServerSocketChannel
- 들어오는 TCP 연결을 수신할 수 있다. 들어오는 연결마다 SocketChannel이 만들어진다

3. Selector

셀렉터를 이용하면 하나의 스레드로 여러 채널을 관리할 수 있다

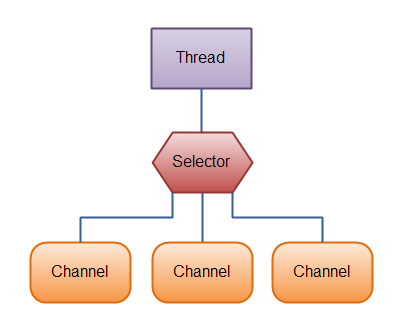
Java NIO: Selectors

셀렉터를 이용하기 위해서는 채널을 셀렉터에 등록해야 한다. 등록 한 뒤 select() 메서드를 호출하면 이 메서드는 등록된 채널 중에 이벤트가 준비된 것이 있을 때 까지 blocked 될 것이다. 메서드가 리턴된 뒤에 스레드는 이러한 이벤트를 처리할 수 있다.

ref. doc

ref.jenkov blog

ref. javatpoint

Comment Read more

BOJ 2667번 단지번호 붙이기(DFS)

20 Mar 2020 | Algorithm

import java.util.Arrays;
import java.util.Scanner;

public class BOJ_2667_DFS {

    static int[][] map;
    static int n;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        map = new int[n][n];
        for (int i = 0; i < n; i++) {
            String s = sc.next();
            for (int j = 0; j < n; j++) {
                map[i][j] = Integer.parseInt(s.charAt(j) + "");
            }
        }
        solve();
    }

    private static void solve() {
        int team = 1;

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (map[i][j] == 1)
                    dfs(i, j, ++team);
            }
        }
        System.out.println(Arrays.toString(map[0]));
        System.out.println(Arrays.toString(map[1]));
        System.out.println(Arrays.toString(map[2]));
        System.out.println(Arrays.toString(map[3]));
        System.out.println(Arrays.toString(map[4]));
        System.out.println(Arrays.toString(map[5]));
        System.out.println(Arrays.toString(map[6]));

        int[] count = new int[team - 1];

        for (int k = 0; k < n; k++) {
            for (int l = 0; l < n; l++) {
                if (map[k][l] > 1)
                    count[map[k][l] - 2]++;
            }
        }

        Arrays.sort(count);

        System.out.println(team - 1);
        for (int h = 0; h < count.length; h++) {
            if (count[h] != 0)
                System.out.println(count[h]);
        }

    }

    static int[] goX = {0, 1, 0, -1};
    static int[] goY = {-1, 0, 1, 0};

    private static void dfs(int i, int j, int team) {

        map[i][j] = team;

        for (int k = 0; k < 4; k++) {
            int x = i + goX[k];
            int y = j + goY[k];

            if ((-1 < x && x < n) && (-1 < y && y < n) && map[x][y] == 1)
                dfs(x, y, team);
        }
    }
}

Comment Read more

BOJ 1012번 유기농 배추

20 Mar 2020 | Algorithm

package BOJ._0319;

import java.util.Scanner;

public class BOJ_1012 {

    static int[][] field;
    static int x;
    static int y;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int t = sc.nextInt();
        while (t-- > 0) {
            x = sc.nextInt();
            y = sc.nextInt();
            int n = sc.nextInt();
            field = new int[x][y];
            for (int i = 0; i < n; i++) {
                int x1 = sc.nextInt();
                int y1 = sc.nextInt();
                field[x1][y1] = 1;
            }
            solve();
        }
    }

    private static void solve() {
        int adjField = 1;
        for (int i = 0; i < x; i++) {
            for (int j = 0; j < y; j++) {
                if (field[i][j] == 1)
                    dfs(i, j, ++adjField);
            }
        }

        System.out.println(adjField - 1);

    }

    static int[] goX = {1, 0, -1, 0};
    static int[] goY = {0, 1, 0, -1};

    private static void dfs(int i, int j, int adjField) {

        field[i][j] = adjField;

        for (int k = 0; k < 4; k++) {
            int x1 = i + goX[k];
            int y1 = j + goY[k];

            if ((-1 < x1 && x1 < x) && (-1 < y1 && y1 < y) && (field[x1][y1] == 1))
                dfs(x1, y1, adjField);
        }

    }
}

Comment Read more

BOJ 1260번 DFS와 BFS

18 Mar 2020 | Algorithm

import java.util.*;

public class BOJ_1260 {

    static boolean[] check;
    static ArrayList<Integer>[] list;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int start = sc.nextInt();

        list = new ArrayList[n + 1];
        check = new boolean[n + 1];
        for (int i = 1; i <= n; i++) {
            list[i] = new ArrayList<>();
        }

        for (int i = 1; i <= m; i++) {
            int from = sc.nextInt();
            int to = sc.nextInt();
            list[from].add(to);
            list[to].add(from);
        }

        for (int i = 1; i <= n; i++) {
            Collections.sort(list[i]);
        }

        dfs(start);
        System.out.println();
        Arrays.fill(check, false);
        bfs(start);
        System.out.println();

    }

    private static void dfs(int u) {

        if (check[u])
            return;

        check[u] = true;

        System.out.print(u + " ");

        for (int v : list[u]) {
            if (!check[v])
                dfs(v);
        }
    }

    private static void bfs(int u) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(u);
        check[u] = true;
        while (!queue.isEmpty()) {
            int v = queue.remove();
            System.out.print(v + " ");
            for (int adj : list[v]) {
                if (!check[adj]) {
                    check[adj] = true;
                    queue.add(adj);
                }
            }
        }
    }

}

Comment Read more

그래프

17 Mar 2020 | Algorithm

그래프

그래프

자료구조의 일종
정점(Vertex)과 간선(Edge)을 가진다
정점의 차수(degree)는 정점에 연결된 간선의 개수이다
G = (V,E)로 나타냄
- V = {a, b, c, d, e}
- E = {ab, ac, bd, cd, de}
인접
- 두 정점이 간선으로 연결되어 있으면 인접해있다고 말한다
경로
- 두 정점 사이의 간선들을 경로라고 말한다
- ex) a와 d의 경로 : abd, acd
사이클
- 정점 A에서 다시 A로 돌아오는 경로를 사이클이라고 한다
단순 경로와 단순 사이클
- 경로/사이클에서 같은 정점을 재방문 하지 않는 경로/사이클
- 특별한 말이 없으면 단순 경로/사이클을 의미한다

Graph Basics

directed 그래프와 undirected 그래프

간선 간에 방향이 존재하는 것

enter image description here

Multiple Edge

정점 간에 경로가 1개 이상 존재하는 그래프를 Multigraph라 한다

그래프의 구현

1. 인접 행렬

정점의 개수를 V라고 하면 V*V 크기의 2차원 배열을 이용
공간복잡도 : O(V^2)
한 정점과 연결된 모든 간선을 찾는 시간복잡도 : O(V)

Adjacency Matrix Representation

2. 인접 리스트

각각의 정점에 대하여 인접한 정점을 저장
링크드 리스트 이용하여 구현
공간복잡도 : O(E)
한 정점과 연결된 모든 간선을 찾는 시간복잡도 : O(차수)

Adjacency List Representation of Graph

인접 행렬 vs 인접 리스트

정점 (u,v) 가 인접해 있는지 확인해보는 경우

인접 행렬의 시간복잡도 : O(1)

인접 리스트의 시간복잡도 : O(E)

그 외 경우는 인접리스트가 성능적인 이점이 있다

3. 간선 리스트

배열을 이용해서 구현하며, 간선을 모두 저장한다
각 간선의 앞 정점을 기준으로 정렬하고 개수를 센다

E배열에서 i 정점과 연결된 간선을 찾기 위해서 i-1 정점의 갯수와 i정점의 갯수를 더한다
```
for(int i=1; i<vertices; i++){
	cnt[i] = cnt[i-1] + cnt[i];  
}
```
i 정점과 연결된 간선은 cnt[i-1] <= E[edge] < cnt[i] 에 존재하게 된다.

ref. 블로그

Comment Read more

jayyhkwon의 개발공부로그

New IO

JAVA NIO (New IO)

1. 채널과 버퍼

2. Non-blocking IO

3. Selectors

1. 채널

3. Selector

BOJ 2667번 단지번호 붙이기(DFS)

BOJ 1012번 유기농 배추

BOJ 1260번 DFS와 BFS

그래프

그래프

그래프의 구현

1. 인접 행렬

2. 인접 리스트

3. 간선 리스트