jayyhkwon의 개발공부로그

퀵정렬

14 Dec 2019 | Algorithm

퀵 정렬

퀵정렬

  • 합병 정렬과 마찬가지로 퀵 정렬또한 분할 정복을 기반으로 정렬하지만 차이점이 있다.

    • 기준값(pivot)을 사용하는 것
      • 그 기준값을 어떤 것을 사용하냐에 따라 퀵 정렬의 성능을 좌우한다.
    • 합병과정이 없다
      • 자식배열을 합치는 과정에서 또 한번 정렬이 일어나는 합병 정렬과는 달리 정복과정에서 이미 배열이 전체 배열이 정렬되어 합병 과정이 없다.

퀵 정렬을 위해서는 2가지 연산이 필요하다

  1. Partition
  2. QuckSort

Partition

  • 기준값(pivot)의 인덱스를 반환하는 연산 –> 퀵 정렬의 핵심

  • pseudocode는 기준값(pivot)을 배열의 마지막 값을 사용한다.

//pseudocode
Partition(A, p, r){
  x = A[r]; // pivot
  i = p-1;
  for j=p to r-1
    if(A[j] <= x){
      i++;
      exchange A[i] with A[j]
    }
  exchange A[i+1] with A[r]
  return i+1;
}

  • 모든 배열 인덱스 k는 다음과 같은 조건을 만족한다.

    • p<= k <= i 이면 A[k] <= x 이다
    • i+1<=k<=j-1이면 A[k] > x 이다

    • k=r 이면 A[k] =x 이다

    • 즉 i를 기준으로 왼쪽 원소 <A[i], 오른쪽 원소> [i] 가 성립한다.

QuickSort

  • QuickSort는 다음과 같은 방법으로 수행된다.
    1. p<r 인 경우 pivot 인덱스 q를 구한다.
    2. QuickSort(A,p,q-1)를 재귀호출 한다.
    3. QuickSort(A,q+1,r)를 재귀호출 한다.
//pseudocode
QuickSort(A,p,r){
 if(p<r){
   q = partition(A,p,r);
   QuickSort(A,p,q-1);
   QuickSort(A,q+1,r);
 }
}

퀵 정렬 시간 복잡도

  • 퀵 정렬은 partition() 연산이 핵심이라는 말을 글을 시작하며 말했다.

    partion()에 따라 시간복잡도는 다음과 같이 달라진다.

  • 최선의 경우 시간복잡도는 O(nlogn)

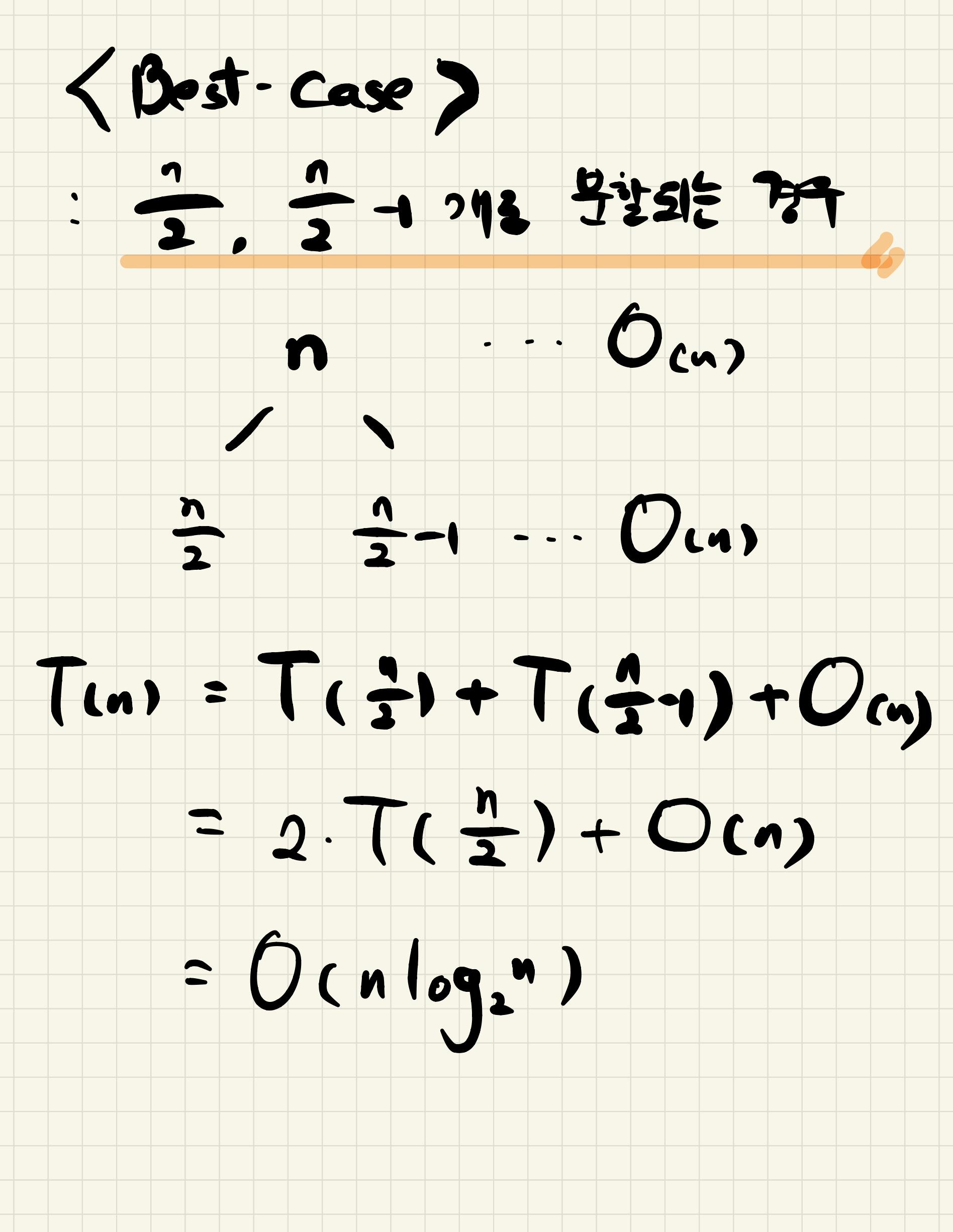
  • 최악의 경우 시간복잡도는 O(n^2)

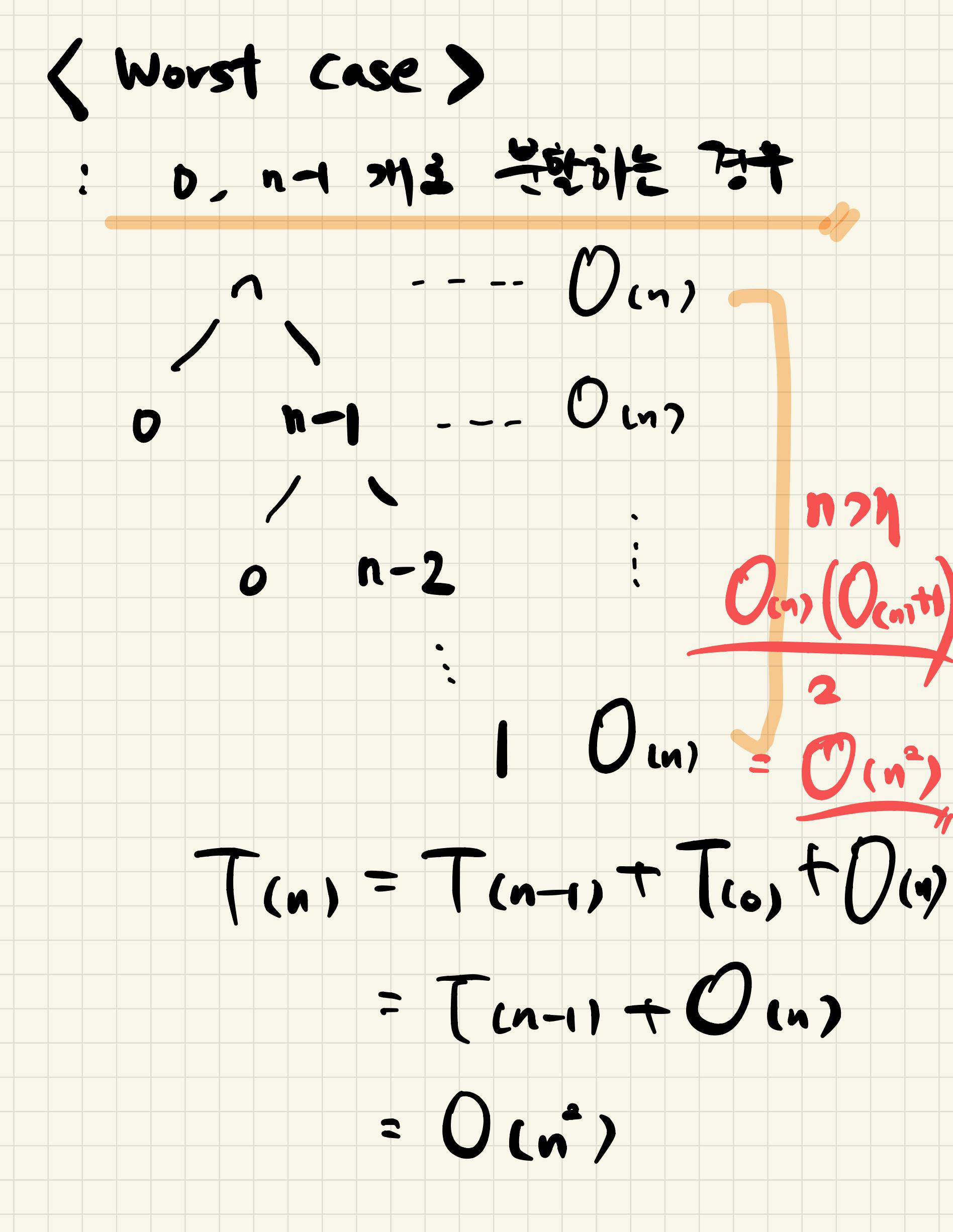
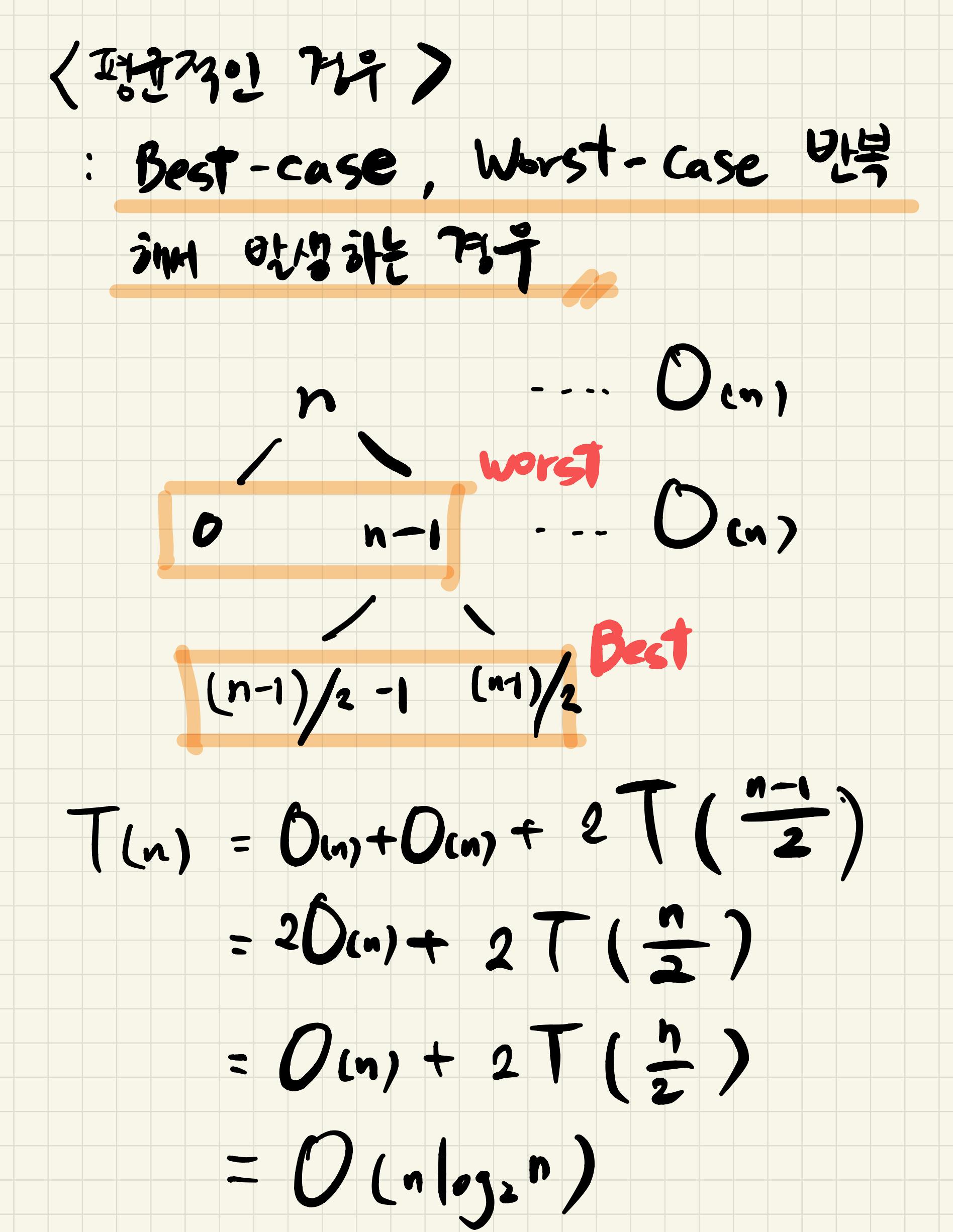
  • 평균의 경우 시간복잡도는 O(nlogn)

Java로 퀵정렬 구현

  • 테스트 코드

import org.junit.jupiter.api.BeforeEach;
import org.junit.jupiter.api.Test;

import static org.junit.jupiter.api.Assertions.assertArrayEquals;

class QuickSortTest {

    private int[] input;
    private int[] output;

    @BeforeEach
    public void setUp(){
        input = new int[]{13,19,9,5,12,8,7,4,21,2,11};
        output = new int[]{2,4,5,7,8,9,11,12,13,19,21};
    }

    @Test
    public void test(){
        QuickSort.quickSort(input,0,input.length-1);
        assertArrayEquals(input,output);
    }
}
  • 알고리즘
public class QuickSort {
    
    public static void quickSort(int[] src, int from, int to){
        if(from < to){
            int mid = partition(src,from,to);
            quickSort(src,from,mid-1);
            quickSort(src,mid+1,to);
        }
    }

    private static int partition(int[] src, int from, int to) {
        int pivot = src[to];
        int i = from -1;
        for(int j=from; j<to ;j++){
            if(src[j] < pivot){
                i++;
                swap(src,i,j);
            }
        }
        swap(src,++i,to);
        return i;
    }

    private static void swap(int[] src, int i, int j) {
        int tmp = src[i];
        src[i] = src[j];
        src[j] = tmp;
    }
}

합병정렬 vs 퀵정렬

  • 같은 분할정복 기법을 사용하는 합병정렬과 퀵정렬을 비교해보자

    최악의 경우를 비교해보자면 합병정렬 = O(nlogn), 퀵정렬 = O(n^2) 으로 퀵정렬이 불리해보인다.

    하지만 그럼에도 불구하고 퀵정렬을 많이 사용하는 데는 이유가 있다.

    1. 추가배열을 사용하지 않는점

    2. 랜덤화 퀵정렬로 최악의 경우를 피할 수 있는점
    3. cpu 캐쉬 히트율이 높아 평균적으로 합병정렬보다 높은 성능을 보인다는 점 에서 합병정렬보다 선호된다.

    배열에 같은 값이 존재하고 인덱스가 의미있는 경우 합병 정렬을 고려할 수 있다.

ref 유투브 

ref Introduction to algorithms

ref 합병정렬 vs 퀵정렬

ref.wiki

Related Posts