jayyhkwon의 개발공부로그

힙정렬

11 Dec 2019 | Algorithm

힙정렬

힙정렬이란?

  • 힙이라는 자료구조를 이용한다.

힙이란 ?

  • 힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리[1]를 기본으로 한 자료구조(tree-based structure)로서 다음과 같은 힙 속성(property)을 만족한다.

    • A가 B의 부모노드(parent node) 이면, A의 키(key)값과 B의 키값 사이에는 대소관계가 성립한다.
    • Key[A] > Key[B] : 최대 힙
    • Key[A] < Key[B] : 최소 힙

힙은 다음과 같이 1차원 배열로도 표현이 가능하다.

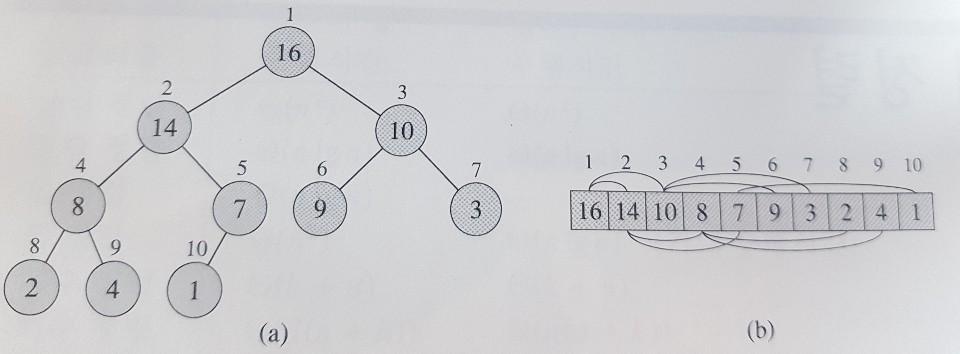
어떤 노드의 인덱스를 index,

왼쪽 자식노드의 인덱스를 left_index,

오른쪽 자식노드의 인덱스를 right_index로 선언하면 다음과 같은 관계를 지닌다.

// 인덱스가 0부터 시작하는 경우
Parent(i) = i/2;

left_index(i) = 2i+1;

right_index(i) = 2i+2;

힙 정렬 알고리즘은 최대힙을 사용하며 3가지 연산이 필요하다.

  1. Max-Heapify
  2. Build Max-Heap
  3. HeapSort

Max-Heapify

  • 최대 힙 특성을 유지하기 위한 연산
  • Max-Heapify를 호출할때 left_index(i), right_index(i)를 루트로 하는 이진트리는 최대 힙이라 가정한다.
  • 시간복잡도는 높이에 비례하므로 O(logn)이다 시간복잡도 증명

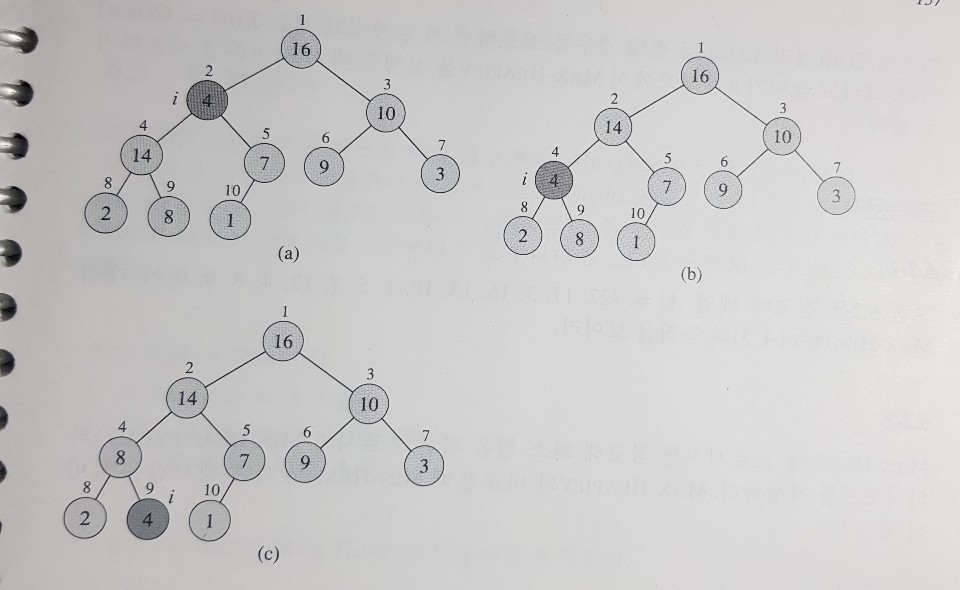
// pseudocode
MaxHeapify(A,i)
	l = left_index(i);
  r = right_index(i);
  if(l <= A.heap_size && A[l] > A[i])
    largest = l;
  else largest = i;
  if(r <= A.heap_size && A[r] > A[largest])
    largest = r;
  if(largest != i)
    exchange A[i] with A[largest]
    MaxHeapify(A,largest);

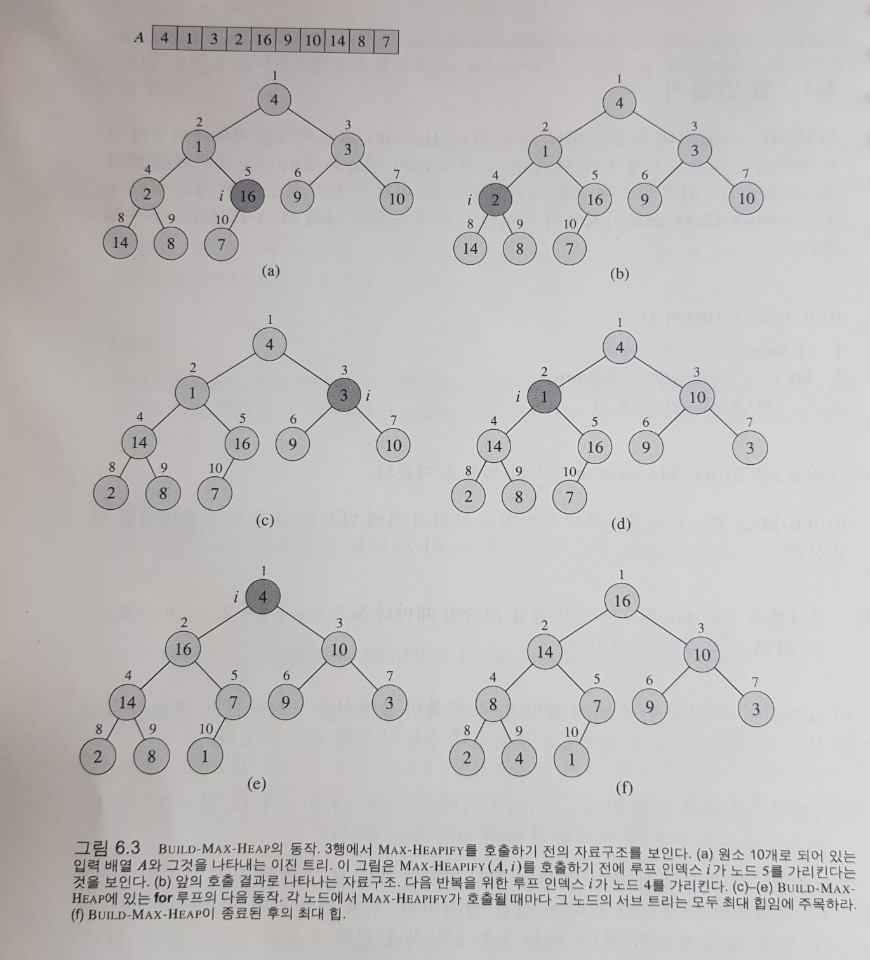
Build Max-Heap

  • 임의의 배열을 최대 힙으로 구성하는 연산
// pseudocode
BuildMaxHeap(A)
  A.heap.size = A.length
  for i=A.length/2 downto 1
    MaxHeapify(A,i)

  • i=length/2부터 시작하는 이유는 length/2+1부터는 리프 노드이므로 MaxHeapify가 필요 없기 때문이다

  • 시간복잡도는 O(logn) * n/2 이므로 O(nlogn)이나, 이것은 루트 노드를 기준으로 러프하게 계산한 것이므로

    좀 더 정확하게 계산하면 O(n)이다.

    참고자료1,참고자료2

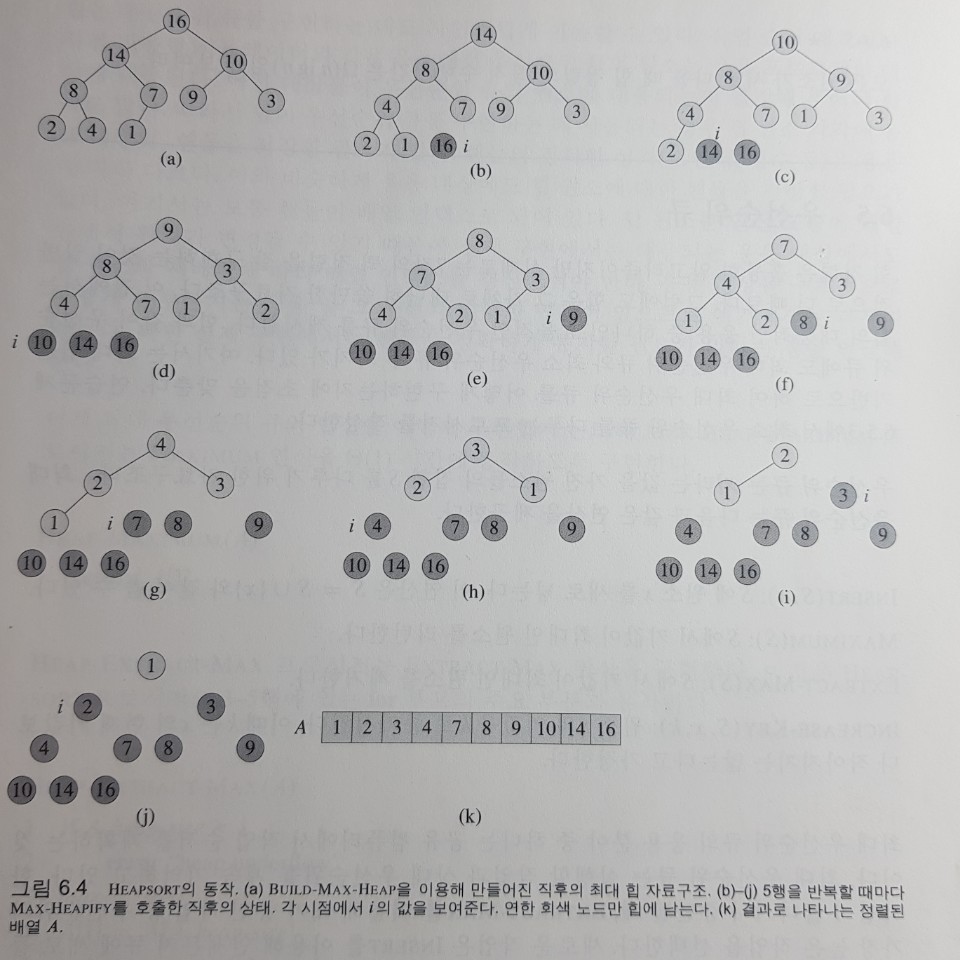
HeapSort

  • 힙 정렬은 다음과 같은 방법으로 수행된다

    1. 주어진 데이터를 힙으로 만든다.
    2. 힙에서 최대값(루트 노드)을 가장 마지막 값과 바꾼다.
    3. 힙의 크기가 1 줄어든 것으로 간주한다. 즉, 마지막 값은 힙의 일부가 아닌것으로 간주한다.
    4. 루트 노드에 대해서 HEAPIFY(1)한다.
    5. 2~4번을 반복한다.

  • 시간복잡도는 O(n) + O(nlogn) = O(nlogn)

    ​

HeapSort(A)
  BuildMaxHeap(A) // O(n)
  for i= A.length downto 2 // O(nlogn)
    exchange A[1] with A[i]
    A.heap.size = A.heap.size - 1
    MaxHeapify(A,1)

Java로 힙정렬 구현

  • 테스트 코드
import org.junit.jupiter.api.Test;
import java.util.Arrays;
import static org.junit.jupiter.api.Assertions.*;

class HeapSortTest {

    @Test
    public void test() {
        int[] input = new int[]{5, 13, 2, 25, 7, 17, 20, 8, 4};
        HeapSort.Heap heap = new HeapSort.Heap(input);
        int[] answer = Arrays.copyOf(input, input.length);
        Arrays.sort(answer);

        HeapSort.heapSort(heap);
        assertArrayEquals(heap.getHeap(), answer);
    }
}
  • 알고리즘

public class HeapSort {

    // 최대힙의 0번째 값(최대값)을 가장 뒤로 보내 정렬한다.
    public static void heapSort(Heap heap){
        buildMaxHeap(heap);
        int tmp = Integer.MIN_VALUE;
        for(int i = heap.length()-1; i>=0; i--){
            swap(heap,i,0);
            heap.decrementSize();
            maxHeapify(heap,0);
        }
    }

    private static void buildMaxHeap(Heap heap){
        for(int i = heap.length()/2-1; i>=0; i--)
            maxHeapify(heap,i);
    }

    private static void maxHeapify(Heap heap, int idx){
        int leftIndex = getLeftIndex(idx);
        int rightIndex = getRightIndex(idx);
        int size = heap.size();
        int largest = -1;

        // 왼쪽 노드와 비교
        if(leftIndex < size && heap.get(leftIndex) > heap.get(idx))
            largest = leftIndex;
        else
            largest = idx;
        // 오른쪽 노드와 비교
        if(rightIndex < size && heap.get(rightIndex) > heap.get(largest))
            largest = rightIndex;
        // 부모 노드보다 자식노드가 큰 경우 교환
        if(largest != idx){
            swap(heap, idx, largest);
            //재귀호출
            maxHeapify(heap,largest);
        }
    }

    private static void swap(Heap heap, int to, int from) {
        int tmp = heap.get(to);
        heap.set(to, heap.get(from));
        heap.set(from, tmp);
    }

    private static int getLeftIndex(int idx){
        return 2*idx+1;
    }

    private static int getRightIndex(int idx){
        return 2*idx+2;
    }

    public static class Heap {
        int[] heap;
        int size;

        public Heap(int[] src){
            heap = src;
            size = heap.length;
        }

        public int size(){
            return size;
        }

        public int length(){
            return heap.length;
        }

        public void decrementSize(){
            size--;
        }

        public int get(int idx){
            return heap[idx];
        }

        public int[] getHeap(){
            return heap;
        }

        public void set(int idx, int value){
            heap[idx] = value;
        }
    }

}

[1]

  • 완전이진트리(complete binary tree)
    • 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있다. 마지막 레벨 h 에서 1부터 2h-1 개의 노드를 가질 수 있다.
  • 포화이진트리(perfect binary tree)
    • 모든 내부 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 깊이 또는 레벨을 갖는다

img

ref. 이진트리 이미지

ref. Introduction to Algorithm

Related Posts