mergeSort 시간복잡도

합병 정렬 시간복잡도 분석

• 입력크기가 n인 배열의 정렬 수행시간을 T(n)이라 하자.

T(n)에 대한 점화식은 다음과 같다.

T(n) = cn ( n = 1 )

T(n) = 2T(n/2) + cn ( n>1 )

T(n)이 2T(n/2) + cn (n>1)인 이유

T(n/2) : n을 divide & conquer 하는 과정

cn : divide & conquer 후 merge하는 데 드는 비용

c : 연산시간, n: 입력크기

• 점화식을 트리구조로 표현하면 다음과 같다.

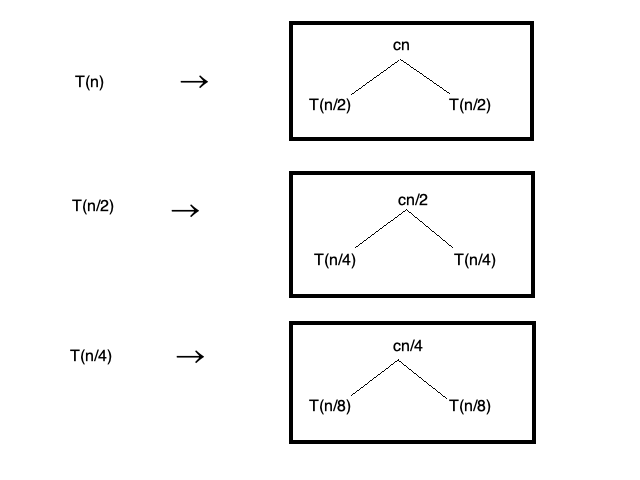
위 그림에서 T(n)을 표현한 트리에서 T(n/2), T(n/4)을 대입하면 다음과 같다.

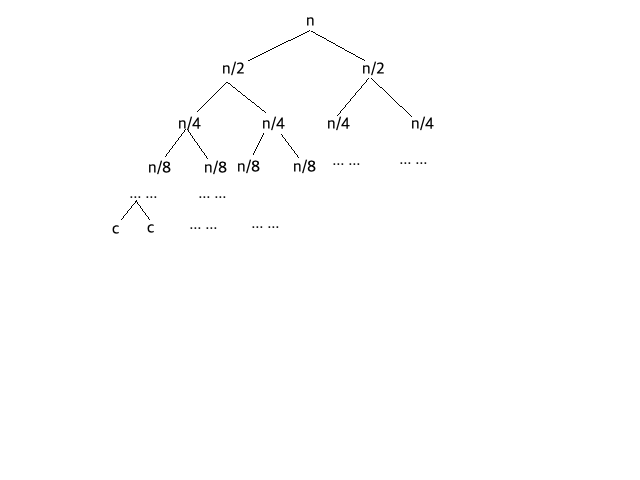
트리의 각 레벨에서 노드의 개수와 각 레벨의 합을 구하면 아래와 같다.

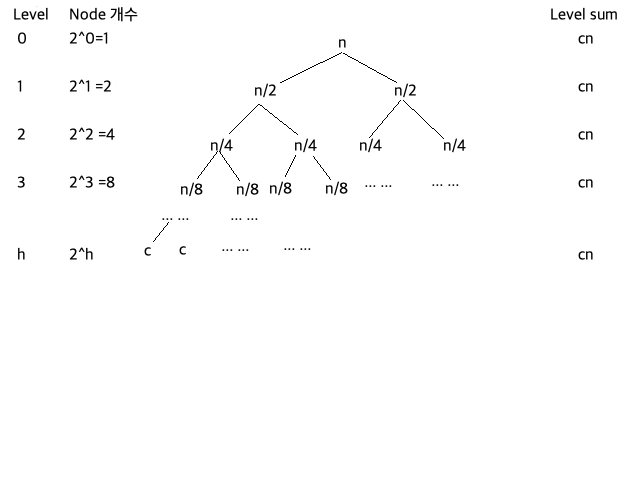
Level 0 에는 n이 1개 있고, level 1 에는 n/2 이 2개, level 2 에는 n/4 이 4개, … , level h 에는 T(1) 이 2^h 개 있다. T(1) = 1 로 표현 가능하므로 h = log2n 이라는 결과를 얻을 수 있다.

2^h * c = cn
2^h = n
h = logn

각 레벨 합이 cn이 트리의 높이 logn 만큼 있으므로
시간 복잡도 = O(nlogn) (c는 상수이므로 생략)